用于绝缘体上硅纳米光子波导的偏振无关光栅耦合器外文翻译资料

英语原文共 3 页，剩余内容已隐藏，支付完成后下载完整资料

796 OPTICS LETTERS / Vol。 36日，2011年3月15日，6号

用于绝缘体上硅纳米光子波导的偏振无关光栅耦合器

夏晨和曾钰成*

香港中文大学电子工程系，中国香港，中国*通讯作者：hktsang@ee.cuhk.edu.hk

收到2010年12月10日; 2011年1月20日修订; 2011年1月29日接受; 2011年2月8日发布（Doc。ID 139464）; 2011年3月7日发布

我们建议在波导光栅中使用亚波长结构，以实现光纤和绝缘体上硅（SOI）光波导之间的偏振无关的光的配光。亚波长结构允许精确设计光栅部分中TE和TM模式的模式有效指标。我们计算出，使用单模光纤与SOI纳米光子波导之间的偏振无关耦合的提出的设计，可以实现超过64％的耦合效率。 copy;2011美国光学学会

OCIS代码：130.0130,050.2770,050.6624。

波导光栅耦合器由于其在平面外的光纤芯片耦合方案中的优势而非常有意义[1-7]。然而，以前报道的所有光纤芯片光栅系统都是强极化反射，耦合到纳米光子波导的TE模式[1-5]或TM模式[6,7]。在许多实际应用中，极化依赖是不希望的，因为通常部署在光网络中的光纤不能保持光的偏振状态。偏振分集方案是解决通用波导光栅耦合器固有极化依赖性的一种可行方法[8]。可以通过偏振光束分离光栅耦合器[9-11]实现光子集成电路的极化独立运算，将TE和TM偏振光耦合到两组相同的纳米光子波导电路中。这具有将设备的占地面积几乎翻倍并且对制造过程施加严格要求以确保两组光电路相同的缺点。

实现偏振无关光子器件如轨道谐振器[12]和波导[13]已经有很多工作。最近也研究了非极化非亚微米波导[14]。在本信中，我们提出了一种偏振无关光纤芯片光栅耦合器，用于折射率工程的优化亚波长结构。据我们所知，这是可以实现偏振无关操作的第一个光栅耦合器设计。虽然以前已经研究了偏振独立光栅[15]，但它只是用于光的平面外衍射的一维（1D）光栅，而不是光纤芯片耦合。 TE和TM模式的衍射角在[15]中仍然不同。

通常在1D光栅中，TE模式有效指数大于TM模式，因为限制因子较大。因此，根据相位匹配条件，耦合到波导的TE模式的光栅周期因此总是小于TM模式所需的周期：

0146-9592/11/060796-03$15.00/0

其中ko =2pi;=lambda;，nc是包层的折射率（对于氧化物等于1.45），theta;是输出光与绝缘体上硅（SOI）晶片的表面法线的角度，neff avg是光栅的平均模式有效指数，q是整数（对于光栅坐标系等于1），Lambda;是波导光栅周期。对于下面段落中索引n的下标，“L”和“H”分别表示低折射率区域（凹槽）和高位置（齿），“eff”表示模式有效指数， “平均”是指平均指数。

为了实现偏振无关光栅，需要一种新的结构来反转正常情况，并使得TM模式有效指数大于特定区域的TE模式有效指数。这可以通过以前提出的亚波长结构[6]和实验证明[7,16,17]来实现，以使得光栅耦合器能够被制造，而不需要单独的浅蚀刻来定义光栅。亚波长光栅耦合器的示意图如图1所示。波导光栅制造在具有340nm厚的顶部硅层和2mu;m厚的掩埋氧化物（BOX）层的SOI晶片上。使用长度为500mu;m的锥形作为横向尺寸转换器来连接纳米光子波导和10微米宽的波导光栅，具有可忽略的损耗。 10mu;m宽的波导光栅具有与光纤（SMF-28）相似的横向模式宽度[4]。光被光栅衍射并耦合到光纤中。通常包括光纤轴与晶片表面法线之间的小角度theta;以避免大的布拉格反射[2]。

图.（在线颜色）（a）具有亚波长结构的偏振无关光纤芯片光栅耦合器的三维示意图.（b）原理图俯视图.（c）示意图。

正方形孔的亚波长尺寸和y轴的周期Lambda;y小于传播光的波长，这允许采用零级的有效介质理论（EMT）近似于 通过具有折射率nL的凹槽的结构，如图1所示。 1（c）[6,16]：

似槽的折射率，如

图.1（c），其中nhole等于1.45，nSi等于3.47。 横向填充因子由f y表示。 不过这个当定义为R = neffLambda;y=lambda;的周期波长比远小于1时，零阶逼近仅是准确的。这里，neff是340nm厚度的平板波导中有效的infx模式（我们 也使用neff TE和neff TM分别表示TE模式和TM模式的相同值）。 更准确的ap-

如果横向特征尺寸与介质中的波长相同，则可以使用采用二阶EMT的近似[18,19]：

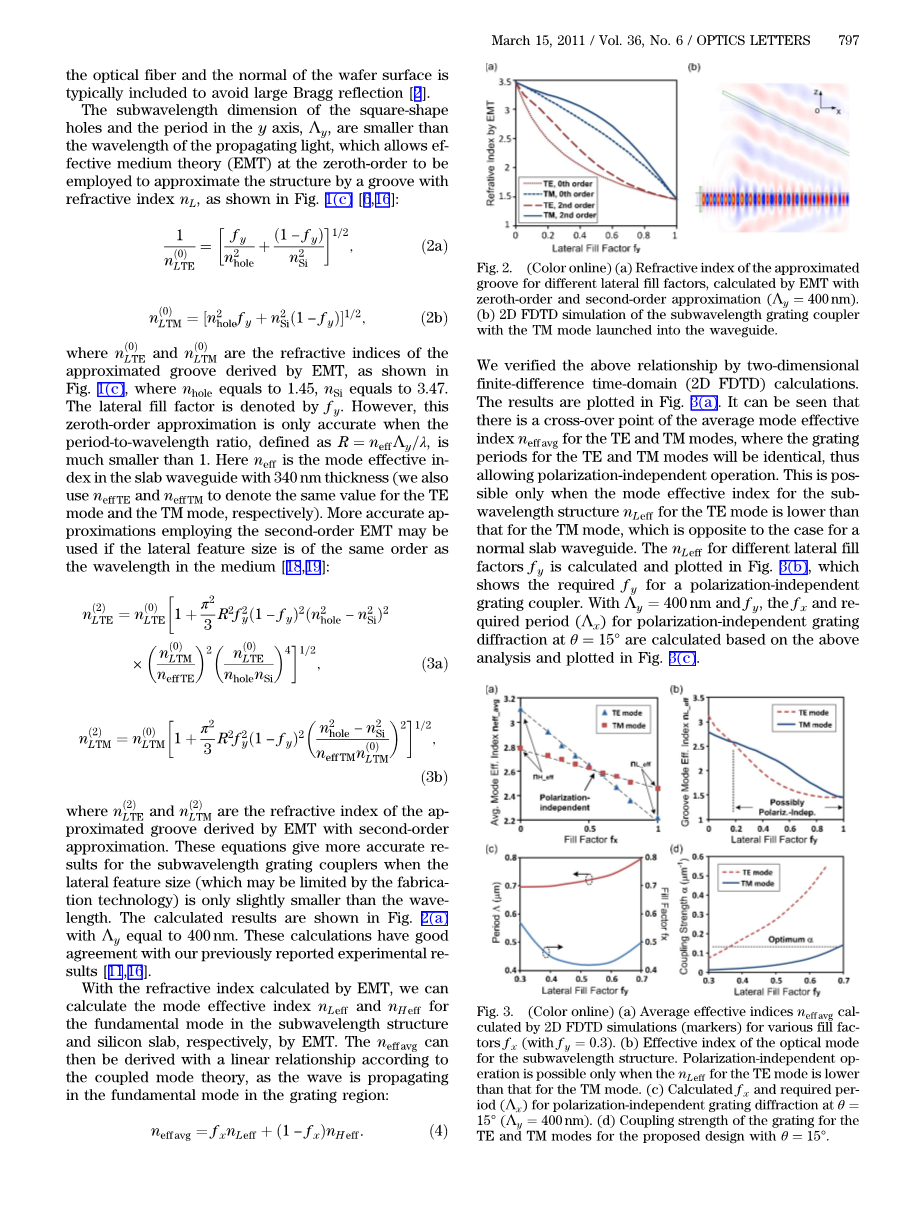
其中neth;L2TETHORN;和neth;L2TMTHORN;是由具有二阶近似的EMT导出的近邻凹槽的折射率。 当横向特征尺寸（可能受制造技术限制））仅略小于波长时，这些方程给出了亚波长光栅耦合器的更准确的结果。 计算结果如图2所示。 2（a）Lambda;y等于400nm。 这些计算与我们以前报告的实验结果有很好的一致性[11,16]。

利用EMT计算的折射率，我们可以分别通过EMT计算亚波长结构和硅片中的基模的模式有效指数nL eff和n H eff。 然后可以根据耦合模式理论以线性关系导出neff平均值，因为波在光栅区域的基本模式中传播：

（4）

图.2 （在线颜色）（a）用于不同横向填充因子的近似凹槽的折射率，通过具有零级和二阶近似（Lambda;y= 400nm）的EMT计算。

（b）具有TM模式的亚波长光栅耦合器的2D FDTD模拟发射到波导中。

我们通过二维有限差分时域（2D FDTD）计算验证了上述关系。结果绘制在图1中。 3（a）。可以看出，平均模式的交叉点有效

因此，TE和TM模式的指数neff平均值，TE和TM模式的光栅周期将相同

允许偏振无关操作。只有当TE模式的子波长结构nLeff的模式有效索引低于TM模式的模式有效索引时，这是正确的，这与普通平板波导的情况相反。计算不同横向填充因子f y的nLeff，并绘制在图1中。图3（b），其示出了偏振无关光栅耦合器所需的f y。对于Lambda;y= 400nm和f y，基于上述分析计算出在theta;= 15°处的偏振非依赖光栅衍射的f x和re-quired周期（Lambda;x），如图1所示。图3（c）。

图.3 （在线颜色）（a）通过用于各种填充因子f x（f y = 0：3）的2D FDTD模拟（标记）计算的平均有效指数neff平均值。 （b）亚波长结构的光学模式的有效指标。 只有当TE模式的nLeff低于TM模式时，才能进行极化独立运算。 （c）在theta;= 15°（Lambda;y= 400nm）处计算fx和对于偏振无关光栅衍射所需的每碘（Lambda;x）。 （d）所提出的设计的TE和TM模式的光栅的耦合强度为theta;= 15°。

为了优化光栅调焦器的耦合效率，耦合强度需要在0:13mu;m-1左右，用于耦合到光纤[4]。然而，对于所提出的设计，TE模式的耦合强度总是强于TM模式，如图1所示。由于在波导光栅中的TE模式的较大折射率步长，因此图3（d）所示。通过在TE和TM模式的耦合强度之间进行折衷，可以实现偏振无关光栅耦合器的优化。我们使用2D FDTD模拟对于x-z平面中的光栅结构，以获得各种横向填充因子f y [6]的耦合效率。对于具有不同极化和耦合强度的每种情况，纤维位置L（定义为纤维芯的中心与x轴上的光栅前端之间的距离）也需要优化。一些结果如图1所示。 4（a）。

如图4（a）所示，我们可以看到，在增加TM模式的效率的同时，增加的速度将降低TE模式的最大耦合效率。用于偏振无关耦合效率的交叉点用f y = 0，6，0.65和0.7用圆圈标注在图中。该模拟预测，可以在使用f = 0:65的偏振非依赖光栅耦合器中实现超过40％的调光效率。该周期为750nm，填充因子f x为0.39。我们从FDTD模拟中发现，对图1所示的计算结果将需要小的校正。 3为f ygt; 0：6，因为布拉格光栅在波导光栅中为TE模式引起相当强的反向传播波。

优化光栅设计的耦合效率如图1所示。 4（b）。 通过三维FDTD模拟获得一致的结果。 分别在TE模式和TM模式下，在1550nm波长处的波导的反射率分别为10％和0.8％。 我们还在光栅中引入了包括两层硅的底部布拉格反射器耦合器[2]。 底部反射器位于光栅耦合器下方1：4mu;m处，并被二氧化硅分离。 包括底部反射器在内的计算的耦合效率也绘制在图1中。 4（b）。 计算预测TE和TM模式的耦合效率超过64％是可能的，并且存在约65nm的3dB光学带宽。

总而言之，我们首次向我们展示了如何在SOI平台上实现偏振无关的光纤芯片光栅耦合器。 亚光束光栅用于使用二阶EMT来设计TE和TM模式的有效输入。 FDTD模拟预测，提出的设计可以实现具有超过64％耦合效率和65nm 3 dB带宽的偏振依赖耦合效率。

这项工作得到了中国香港大学教育资助委员会的支持，特别是中大香港特别设备津贴基金和GRC 416710。

参考

1.D. Taillaert，W.Bogaerts，P.Bienstman，T.F.Krauss，P.Van Daele，I.Moerman，S.Verstuyft，K.Deelel和R.Baets，IEEE J.Quantum Electron。 38,949（2002）。

2.D. Taillaert，P. Bienstman和R. Baets，Opt。快报。 29，2749（2004）。

3.Y. Tang，Z.Wang，L.Wosinski，U.Westergren和S.He，Opt。快报。 35，1290（2010）。

4.X. Chen，C.Li，C.K.Y.Fung，S.M.G.Lo，and H.K.Tang，IEEE Photon。 TECHNOL。快报。 22，1156（2010）。

5.D. Vermeulen，S. Selvaraja，P. Verheyen，G.Lepage，W.Bogaerts，P.Absil，D.Van Thourhout和G.Roelkens，Opt。 Express 18,18278（2010）。

6.R. Halir，P. Cheben，S. Janz，D.-X。 Xu，I.Molina-Fernandez和J.G.Wanguemert-Perez，Opt。快报。 34，1408（2009）。

7.R. Halir，P. Cheben，J.H.Schmid，R.Ma，D.Beard，

S·詹斯，D.-X.徐A.登斯莫尔，J·拉波因特和

莫里纳 - 费尔南德斯快报。 35，3243（2010）。

8.W. Bogaerts，D. Taillaert，P.Dumon，D. Van Thourhout，

R.Baets和E.Pluk，Opt。 Express 15，1567（2007）。

9.D. Taillaert，H.Chang，P.I.Borel，L.H.Frandsen，R.M.De La Rue和R.Betets，IEEE Photon。 TECHNOL。快报。 15,1249（2003）。

10.J. Feng和Z. Zhou，选择快报。 32，1662（2007）。

11.x的Chen，C.Li，and H.K.Zang，Opt。 COMMUN。 283，2146（2010）。

12.W. R. Headley，G.T.Reed，S.Howe，A.Liu，和M.Paniccia，Appl。物理学。快报。 85，5523（2004）。

13.S. P.Chen，C.E.Png，S.T.Lim，G.T.Reed，和V.M.N.Passaro，J.Lightwave Technol。 23，2103（2005）。

14.S. T.Lim，C.E.Png，E.A.Ogg和Y.L.Ang，Opt。 Express 15，11061（2007）。

15.S. Shao and Y. Wang，Opt。快报。 35，1834（2010）。

16.X.陈和曾光辉，IEEE Photon。 J. 1,184（2009）。

17.L. Liu，M.Pu，K.Yvind和J.M.Hvam，Appl。物理学。快报。 96，051126（2010）。

18.S.索夫夫·雷托夫物理学。 JETP 2，466（1956）。

19.D. H.Raguin和G.M.Morris，Appl。选择。 32，1154（1993）。

Cānkǎo

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[25673]，资料为PDF文档或Word文档，PDF文档可免费转换为Word